18.2 Cox 의 비례위험모형(수정중)

생존함수와 위험함수

생존함수 S(t) survival function

   생존할 확률

   t시점까지 생존할 (누적생존)확률 cumulatie survival rate

   처음에는 확률이 1로 시작하여 시간에 따라 감소함수... 

 

위험함수 hazard funtion

   t 시간까지 생존한 사람이 그 시점에서 사망할 (순간) 위험도

   위험함수는 줄어들기도 하고, 증가하기도 하고, 일정하기도 하고
   생존분석에서는 이 위험함수 => 일반화선형모형에 적합화 => 생존율에 영향을 주는 인자임을 파악

 

   예) - 가전 제품을 처음 사면 고장률이 높다가 점차 감소하다, 일정시간 동안 고장률이 일정하다가

        오래 되면 고장율이 증가하는 것과 비슷
        - 새로이 아파트에 입주하면 하자보수를 하느라고 고장률이 높은 상태

          하자보수 기간이 끝나면, 안정권으로 접어 들다가, 세월이 지나면서 노후화되면

          고장률이 증가

 

위험함수 추정 방법 - 모수적방법, 비모수적 방법

모수적 방법 - 생존시간 분포가 일정한 형태...

    지수분포, 곰페르츠 분포, 와이블 부노 등

 

지수분포

   "사망의 위험률이 시간에 따라 일정하다..." 가정   
   생존함수가 지수형태로 감소... 

tongcon 생각 이 부분이 오래동안 헷갈리는 부분이었음

곰페르츠 분포

   위험률이 시간에 따라 선형함수 가정

와이블 분포

   위험률이 로그함수임을 가정????

 

참고: 일반화선형모형과 이를 추정하는 방법

    비모수적 방법

 

Cox 비례위험모형 proportional hazarad model,  PH model

 

1972년 Cox가 제안

생존시간 분포에 대한 가정을 하지 않음

Hazard Function 에 대한 독립변수 영향 관련, 일부 가정 고려... 준모수적 방법 

 

무슨 비례?

비율(비례위험도)  = 위험인자가 있는 경우의 위험도/위험이 없는 경우의 위험도  

비례위험도가 시간에 대하여 일정하다고 가정...  가만... 지주분포와 한편으로 비슷?

 

다음과 같은 식으로 설명되는구나... 

 

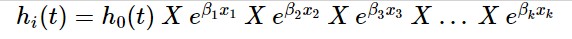
hi(t) :   환자 i 의               t 시점의 사건 발생의 위험도

ho(t) :  위험인자가 없을 때 t 시점의 사건 발생의 위험도

exp(Bk) : 위험인자 k가 있는 경우 비례위험도

 

위험인자가 없는 경우(k=0) 위험도   => exp(0) =1

위험인자가 있는 경우        위험도   => exp(B1), ep(B2), ... exp(Bk)